III. HOME WORK PROBLEMS
3. AN WRONG CLASSIFICATION PROBLEM
Intuitively, we all know that the longer we run the simulation, the smaller
the uncertainty associated with an estimate of, say, the performance J of the
system. Suppose you were told that the uncertainty associated with J
is uniformly distributed about the estimate with half width
w(t) = c/t where c is a constant associated
with the simulation. Now consider two parametrically different but
structurally similar simulation running side-by-side. Their uncertainty
constants are c1 and c2 respectively. Let
the estimates for J be respectively
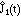 and
and
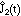 at time t. I would like to stop the simulation at a time when I
observe, say,
at time t. I would like to stop the simulation at a time when I
observe, say,
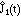 >
>
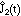 , I can be 90% sure that the actual order is also
J1 > J2 and not J2
> J1. Similarly if it is the other way around.
, I can be 90% sure that the actual order is also
J1 > J2 and not J2
> J1. Similarly if it is the other way around.
- To simplify matters, let us pose an easier problem.
Suppose at some time we observe 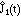 = 1 and
= 1 and 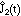 = 2 and from statistical
analysis we also know that w1 = w2 =
c1/t = c2/t = 1.0. What is
the probability that the actual order is J1 >
J2, i.e., the probability of a wrong classification?
= 2 and from statistical
analysis we also know that w1 = w2 =
c1/t = c2/t = 1.0. What is
the probability that the actual order is J1 >
J2, i.e., the probability of a wrong classification?
- Now suppose that you know c1 and c2
you observe
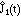 and
and 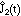 , describe a procedure (as the function of
time) by which you can be 90% sure that the observe order is in fact the
correct order? (describe only the main idea, you are not required to work out
the details).
, describe a procedure (as the function of
time) by which you can be 90% sure that the observe order is in fact the
correct order? (describe only the main idea, you are not required to work out
the details).
[Hint: consider the probability of wrong classification and the
below diagram.]
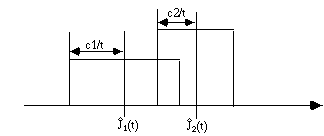
Fig. 1 Possibilities of wrong classification
- Is the above figure the only possibility you should consider for part
(ii)? If so or if not, explain your answer.
- Suppose at some time we observe
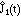 = 1 and
= 1 and 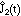 = 2.5 and from
statistical analysis we also know that w1 =
c1/t = 5.0 and w2 =
c2/t = 1.0. What is the probability that the actual
order is J1 > J2, i.e., the probability
of a wrong classification?
= 2.5 and from
statistical analysis we also know that w1 =
c1/t = 5.0 and w2 =
c2/t = 1.0. What is the probability that the actual
order is J1 > J2, i.e., the probability
of a wrong classification?
[Hint: consider the answer to part (iii)]

